Το Πυθαγόρειο θεώρημα

Εδώ είναι ένας χαρακτήρας που κάθε χρόνο δυσκολεύει έναν καλό αριθμό μαθητών γυμνασίου, αλλά και δασκάλων.

Πράγματι, αυτός ο άνθρωπος, πριν από πολύ καιρό, μας άφησε ένα θεώρημα και κάθε χρόνο πολλοί μαθητές προσπαθούν να κατανοήσουν και να θυμηθούν την εξίσωσή του.

Από χρόνο σε χρόνο, οι δάσκαλοί σας πρέπει να σας βοηθήσουν να ανακαλύψετε, να κατανοήσετε και να μάθετε αυτό το θεώρημα.

Θέλω να μιλήσω εδώ για Πυθαγόρας.

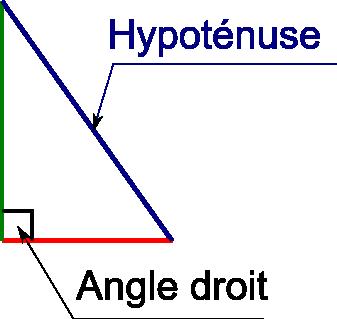
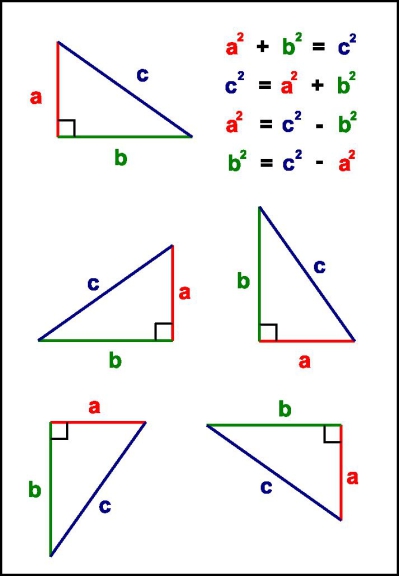
Ο Πυθαγόρειο θεώρημα μπορεί να δηλωθεί ως εξής: « Σε ένα ορθογώνιο τρίγωνο, το τετράγωνο της υποτείνουσας είναι ίσο με το άθροισμα των τετραγώνων των άλλων δύο πλευρών.”

ΜΕΓΑΛΟ’ Υποτείνουσα αντιπροσωπεύει στο ορθογώνιο τρίγωνο, ΘΕ απέναντι πλευρά στοορθή γωνία.

Μπορείτε να παρατηρήσετε ότι ανεξάρτητα από την κατεύθυνση του τριγώνου μας, η εξίσωση δεν αλλάζει, αλλά από την άλλη μπορεί να γραφτεί με διαφορετικούς τρόπους.

Απομένει τώρα να καθορίσουμε πώς θα βρούμε τον αριθμό που, πολλαπλασιασμένος με τον εαυτό του, δίνει το αποτέλεσμα που βρέθηκε στην εξίσωση. (Η τετραγωνική ρίζα)

a x a = a²

b x b = b²

c x c = c²

Εάν δεν έχετε καλύψει ακόμα τον τρόπο υπολογισμού του α τετραγωνική ρίζα, πάρτε την αριθμομηχανή σας και πατήστε το πλήκτρο τετραγωνική ρίζα αντιπροσωπεύεται από αυτό το σύμβολο √

Ένα παράδειγμα για την κατανόηση αυτού του θεωρήματος.

α = 3

b = 4

c = ?

Γνωρίζουμε λοιπόν ότι: a² + b² = c²

a² = 3² = 3 x 3 = 9

b² = 4² = 4 x 4 = 16

a² + b² = c²
9 + 16 = 25

c² = 25

c x c = 25

c = 5